gnark
What's gnark?
gnark is a fast zk-SNARK library that offers a high-level API to design circuits. The library is open source and developed under the Apache 2.0 license
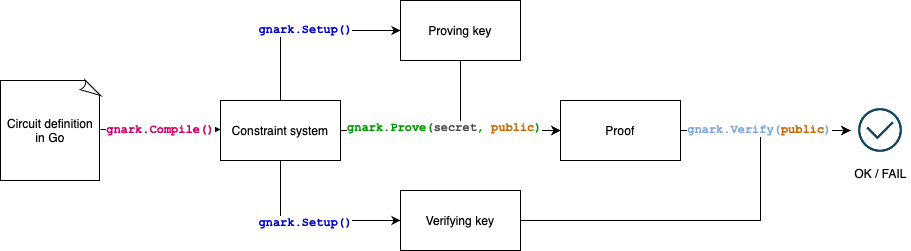
How does gnark work?
In a typical workflow:
- Implement an algorithm for which you want to prove and verify execution.
- Use the
gnark/frontendpackage to translate the algorithm into a set of mathematical constraints. - Use the
gnark/backendpackage to create and verify your proof of knowledge. That is, you prove that you know a list of secret inputs satisfying a set of mathematical constraints.
gnark has been partially audited and is provided as-is, use at your own risk.
In particular, gnark makes no security guarantees such as constant time implementation or side-channel attack resistance.
gnark circuits are written in Go
Users write their zk-SNARK circuits in plain Go. gnark uses Go because:
- Go is a mature and widely used language with a robust tool chain.
- Developers can debug, document, test and benchmark circuits as they would with any other Go program.
- Circuits can be versioned, unit-tested and used in standard continuous integration and delivery (CI/CD) workflows.
- IDE integration.
gnark exposes its APIs like any conventional cryptographic library. Complex solutions need API flexibility. For example gRPC and REST APIs, serialization protocols, monitoring, and logging can be easily added.
- define circuit
- compile circuit
- create proof
- unit test
// Circuit defines a pre-image knowledge proof
// mimc(secret preImage) = public hash
type Circuit struct {
PreImage frontend.Variable
Hash frontend.Variable `gnark:",public"`
}
// Define declares the circuit's constraints
func (circuit *Circuit) Define(api frontend.API) error {
// hash function
mimc, err := mimc.NewMiMC(api.Curve())
// specify constraints
// mimc(preImage) == hash
api.AssertIsEqual(circuit.Hash, mimc.Hash(cs, circuit.PreImage))
return nil
}
var mimcCircuit Circuit
r1cs, err := frontend.Compile(ecc.BN254, r1cs.NewBuilder, &mimcCircuit)
// witness
assignment := &Circuit{
Hash: "16130099170765464552823636852555369511329944820189892919423002775646948828469",
PreImage: 35,
}
witness, _ := frontend.NewWitness(assignment, ecc.BN254.ScalarField())
publicWitness, _ := witness.Public()
pk, vk, err := groth16.Setup(r1cs)
proof, err := groth16.Prove(r1cs, pk, witness)
err := groth16.Verify(proof, vk, publicWitness)
assert := groth16.NewAssert(t)
var mimcCircuit Circuit
{
assert.ProverFailed(&mimcCircuit, &Circuit{
Hash: 42,
PreImage: 42,
})
}
{
assert.ProverSucceeded(&mimcCircuit, &Circuit{
Hash: "16130099170765464552823636852555369511329944820189892919423002775646948828469",
PreImage: 35,
})
}
gnark is fast
gnarkwon the ZPrize competition to accelerate MSM on Mobile 🎉- zka.lc shows gnark performs better than
arkworksorsupranational/blstfor most operations
It is difficult to fairly and accurately compare benchmarks among libraries. Some implementations may excel in conditions where others may not. Results depend on target or available instruction set, CPUs and RAM.
On low-level primitives like the pairing or the field multiplication, gnark-crypto outperforms most libraries out there. It translates well up-the-stack - gnark compiles gigantic circuits in seconds, and its solver (aka witness generation) and provers perform very well on most architectures.
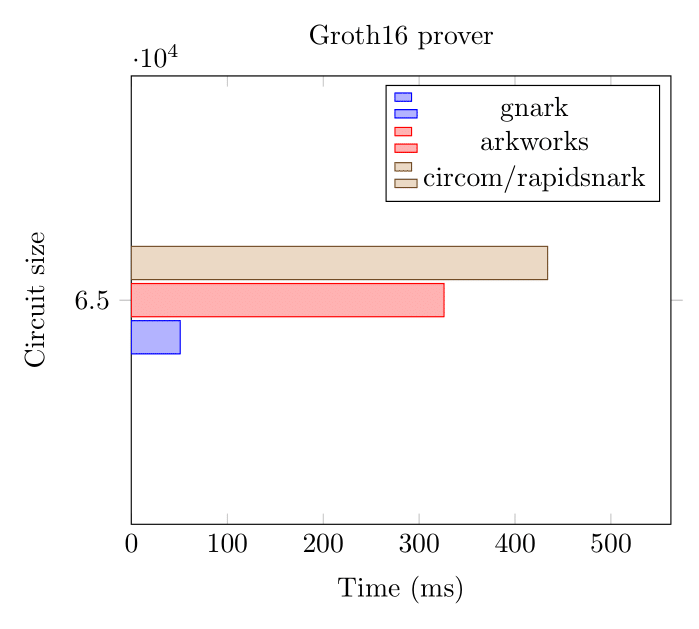
Here we benchmark two circuits (65k and 8M constraints) using gnark, arkworks and rapidsnark on the BN254 curve.
Groth16 Prover (BN254, 65k constraints)
Groth16 Prover (BN254, 8 million constraints)
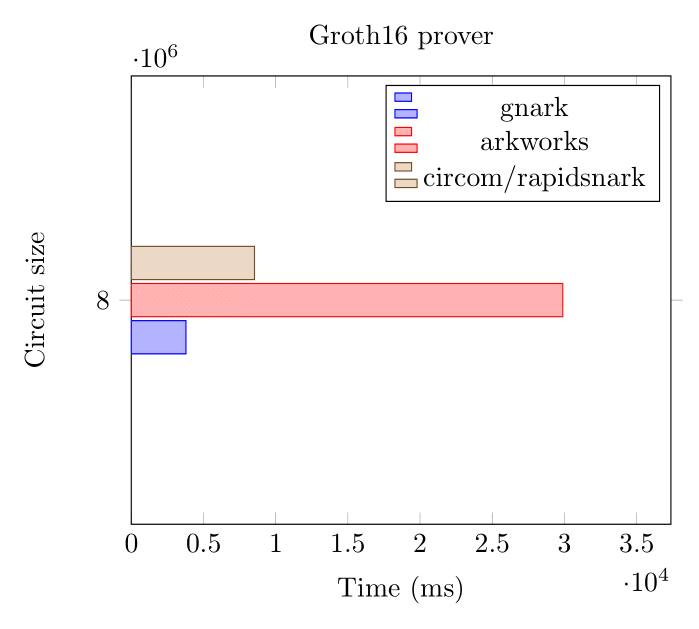
On large circuits, that's over 2 million constraints per second.
Groth16 Verifier (BN254)
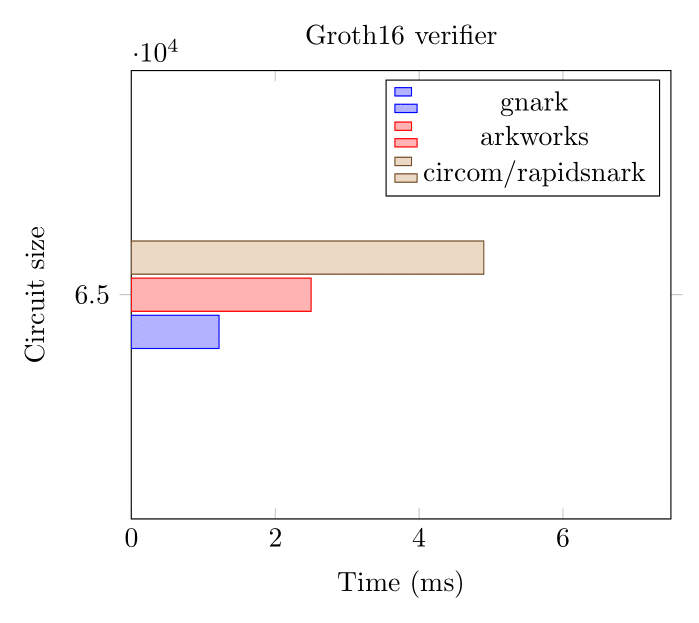
These benchmarks were executed on an AWS hpc6a instance in November 2022.
Proving schemes and curves
Refer to the Proving schemes and curves section.